- Thoroughly revamping handling of posterior predictive nodes in the MCMC system, in particular that MCMC samplers, by default, will now exclude predictive dependencies from internal sampler calculations. This should improve MCMC mixing for models with predictive nodes. Posterior predictive nodes are now sampled conditional on all other model nodes at the end of each MCMC iteration.
- Adding functionality to the MCMC configuration system, including a new replaceSamplers method and updates to the arguments for the addSamplers method.
- Adding an option to the WAIC system to allow additional burnin (in addition to standard MCMC burnin) before calculating online WAIC, thereby allowing inspection of initial samples without forcing them to be used for WAIC.
- Warning users of unused constants during model building.
- Fixing bugs that prevented use of variables starting with ‘logProb’ or named ‘i’ in model code.
- Fixing a bug to prevent infinite recursion in particular cases in conjugacy checking.
- Fixing a bug in simulating from dcar_normal nodes when multiple nodes passed to simulate.
Author Archives: Chris Paciorek
NIMBLE virtual short course, January 4-6, 2023
We’ll be holding a virtual training workshop on NIMBLE, January 4-6, 2023 from 8 am to 1 pm US Pacific (California) time each day. NIMBLE is a system for building and sharing analysis methods for statistical models, especially for hierarchical models and computationally-intensive methods (such as MCMC and SMC).
Recently we added support for automatic differentiation (AD) to NIMBLE in a beta release, and the workshop will cover NIMBLE’s AD capabilities in detail.
The workshop will cover the following material:
- the basic concepts and workflows for using NIMBLE and converting BUGS or JAGS models to work in NIMBLE.
- overview of different MCMC sampling strategies and how to use them in NIMBLE, including Hamiltonian Monte Carlo (HMC).
- writing new distributions and functions for more flexible modeling and more efficient computation.
- tips and tricks for improving computational efficiency.
- using advanced model components, including Bayesian non-parametric distributions (based on Dirichlet process priors), conditional auto-regressive (CAR) models for spatially correlated random fields, Laplace approximation, and reversible jump samplers for variable selection.
- an introduction to programming new algorithms in NIMBLE.
- use of automatic differentiation (AD) in algorithms.
- calling R and compiled C++ code from compiled NIMBLE models or functions.
If you are interested in attending, please pre-register. Registration fees will be $125 (regular) or $50 (student). We are also offering a process (see the pre-registration form) for students to request a fee waiver.
The workshop will assume attendees have a basic understanding of hierarchical/Bayesian models and MCMC, the BUGS (or JAGS) model language, and some familiarity with R.
Beta version of NIMBLE with automatic differentiation, including HMC sampling and Laplace approximation
We’re excited to announce that NIMBLE now supports automatic differentiation (AD), also known as algorithmic differentiation, in a beta version available on our website. In this beta version, NIMBLE now provides:
- Hamiltonian Monte Carlo (HMC) sampling for an entire parameter vector or arbitrary subsets of the parameter vector (i.e., combined with other samplers for the remaining parameters).
- Laplace approximation for approximate integration over latent states in a model, allowing maximum likelihood estimation and MCMC based on the marginal likelihood (via the RW_llFunction samplers).
- The ability for users and algorithm developers to write nimbleFunctions that calculate derivatives of functions, including many but not all mathematical operations that are supported in the NIMBLE language.
We’re making this beta release available to allow our users to test and evaluate the AD functionality and the new algorithms, but it is not recommended for production use at this stage. So please give it a try, and let us know of any problems or suggestions you have, either via the nimble-users list, bug reports to our GitHub repository, or email to nimble.stats@gmail.com.
You can download the beta version and view an extensive draft manual for the AD functionality.
We plan to release this functionality in the next NIMBLE release on CRAN in the coming months.
Version 0.12.2 of NIMBLE released, including an important bug fix for some models using Bayesian nonparametrics with the dCRP distribution
We’ve released the newest version of NIMBLE on CRAN and on our website. NIMBLE is a system for building and sharing analysis methods for statistical models, especially for hierarchical models and computationally-intensive methods (such as MCMC and SMC).
Version 0.12.2 is a bug fix release. In particular, this release fixes a bug in our Bayesian nonparametric distribution (BNP) functionality that gives incorrect MCMC results for some models, specifically when using the dCRP distribution when the parameters of the mixture components (i.e., the clusters) have hyperparameters (i.e., the base measure parameters) that are unknown and sampled during the MCMC. Here is an example basic model structure that is affected by the bug:
k[1:n] ~ dCRP(alpha, n)
for(i in 1:n) {
y[i] ~ dnorm(mu[k[i]], 1)
mu[i] ~ dnorm(mu0, 1) ## mixture component parameters with hyperparameter
}
mu0 ~ dnorm(0, 1) ## unknown cluster hyperparameter
(There is no problem without the hyperparameter layer – i.e., if mu0 is a fixed value – which is the situation in many models.)
We strongly encourage users using models with this type of structure to rerun their analyses, and we apologize for this issue.
Other changes in this release include:
- Fixing an issue with reversible jump variable selection under a similar situation to the BNP issue discussed above (in particular where there are unknown hyperparameters of the regression coefficients being considered, which would likely be an unusual use case).
- Fixing a bug preventing setup of conjugate samplers for dwishart or dinvwishart nodes when using dynamic indexing.
- Fixing a bug preventing use of truncation bounds specified via `data` or `constants`.
- Fixing a bug preventing MCMC sampling with the LKJ prior for 2×2 matrices.
- Fixing a bug in `runCrossValidate` affecting extraction of multivariate nodes.
- Fixing a bug producing incorrect subset assignment into logical vectors in nimbleFunction code.
- Fixing a bug preventing use of `nimbleExternalCall` with a constant expression.
- Fixing a bug preventing use of recursion in nimbleFunctions without setup code.
Please see the release notes on our website for more details.
NIMBLE in-person short course, June 1-3, Lisbon, Portugal
We’ll be holding a in-person training workshop on NIMBLE, June 1-3, 2022, in Lisbon, Portugal, sponsored by the Centro de Estatística e Aplicações at the Universidade Lisboa (CEAUL).
NIMBLE is a system for building and sharing analysis methods for statistical models, especially for hierarchical models and computationally-intensive methods (such as MCMC and SMC).
More details and registration are available at the workshop website. No previous NIMBLE experience is required, but the workshop will assume some familiarity with hierarchical models, Markov chain Monte Carlo (MCMC), and R.
NIMBLE online tutorial, November 18, 2021
We’ll be giving a two-hour tutorial on NIMBLE, sponsored by the environmental Bayes (enviBayes) section of ISBA (The International Society for Bayesian Analysis), on Thursday November 18, from 11 am to 1 pm US Eastern time.
NIMBLE (r-nimble.org) is a system for fitting and programming with hierarchical models in R that builds on (a new implementation of) the BUGS language for declaring models. NIMBLE provides analysts with a flexible system for using MCMC, sequential Monte Carlo, MCEM, and other techniques on user-specified models. It provides developers and methodologists with the ability to write algorithms in an R-like syntax that can be easily disseminated to users. C++ versions of models and algorithms are created for speed, but these are manipulated from R without any need for analysts or algorithm developers to program in C++. While analysts can use NIMBLE as a nearly drop-in replacement for WinBUGS or JAGS, NIMBLE provides enhanced functionality in a number of ways.
Your avatar is your business card. Take high-quality, and better professional photos. Think over your style, add accessories hooksexup. In short, show yourself on the back side.
This workshop will demonstrate how one can use NIMBLE to:
- flexibly specify an MCMC for a specific model, including choosing samplers and blocking approaches (and noting the potential usefulness of this for teaching);
- tailor an MCMC to a specific model using user-defined distributions, user-defined functions, and vectorization;
- write your own MCMC sampling algorithms and use them in combination with samplers from NIMBLE’s library of samplers;
- develop and disseminate your own algorithms, building upon NIMBLE’s existing algorithms; and
- use specialized model components such as Dirichlet processes, conditional auto-regressive (CAR) models, and reversible jump for variable selection.
The tutorial will assume working knowledge of hierarchical models and some familiarity with MCMC. Given the two-hour time frame, we’ll focus on demonstrating some of the key features of NIMBLE, without going into a lot of detail on any given topic.
To attend, please register here.
Version 0.12.1 of NIMBLE released
We’ve released the newest version of NIMBLE on CRAN and on our website. NIMBLE is a system for building and sharing analysis methods for statistical models, especially for hierarchical models and computationally-intensive methods (such as MCMC and SMC).
Version 0.12.1, in combination with version 0.12.0 (which was released just last week), provides a variety of new functionality (in particular enhanced WAIC functionality and adding the LKJ distribution) plus bug fixes affecting MCMC in specific narrow cases described below and that warrant upgrading for some users. The changes include:
- Completely revamping WAIC in NIMBLE, creating an online version that does not require any particular variable monitors. The new WAIC can calculate conditional or marginal WAIC and can group data nodes into joint likelihood terms if desired. In addition there is a new calculateWAIC() function that will calculate the basic conditional WAIC from MCMC output without having to enable the WAIC when creating the MCMC.
- Adding the LKJ distribution, useful for prior distributions for correlation matrices, along with random walk samplers for them. These samplers operate in an unconstrained transformed parameter space and are assigned by default during MCMC configuration.
- Fixing a bug introduced in conjugacy processing in version 0.11.0 that causes incorrect MCMC sampling only in specific cases. The impacted cases have terms of the form “a[i] + x[i] * beta” (or more simply “x[i] * beta”), with beta subject to conjugate sampling and either (i) ‘x’ provided via NIMBLE’s constants argument and x[1] == 1 or (ii) ‘a’ provided via NIMBLE’s constants argument and a[1] == 0.
- Fixing an error in the sampler for the proper CAR distribution (dcar_proper) that gives incorrect MCMC results when the mean of the proper CAR is not the same value for all locations, e.g., when embedding covariate effects directly in the `mu` parameter of the `dcar_proper` distribution.
- Fixing isData(‘y’) to return TRUE whenever any elements of a multivariate data node (‘y’) are flagged as data. As a result, attempting to carry out MCMC on the non-data elements will now fail. Formerly if only some elements were flagged as data, `isData` would only check the first element, potentially leading to other elements that were flagged as data being overwritten.
- Error trapping cases where a BNP model has a differing number of dependent stochastic nodes (e.g., observations) or dependent deterministic nodes per group of elements clustered jointly (using functionality introduced in version 0.10.0). Previously we were not error trapping this, and incorrect MCMC results would be obtained.
- Improving the formatting of standard logging messages.
Posterior predictive sampling and other post-MCMC use of samples in NIMBLE
(Prepared by Chris Paciorek and Sally Paganin.)
Once one has samples from an MCMC, one often wants to do some post hoc manipulation of the samples. An important example is posterior predictive sampling, which is needed for posterior predictive checking.
With posterior predictive sampling, we need to simulate new data values, once for each posterior sample. These samples can then be compared with the actual data as a model check.
In this example, we’ll follow the posterior predictive checking done in the Gelman et al. Bayesian Data Analysis book, using Newcomb’s speed of light measurements (Section 6.3).
Posterior predictive sampling using a loop in R
Simon Newcomb made 66 measurements of the speed of light, which one might model using a normal distribution. One question discussed in Gelman et al. is whether the lowest measurements, which look like outliers, could have reasonably come from a normal distribution.
Setup
We set up the nimble model.
library(nimble, warn.conflicts = FALSE) code <- nimbleCode({ ## noninformative priors mu ~ dflat() sigma ~ dhalfflat() ## likelihood for(i in 1:n) { y[i] ~ dnorm(mu, sd = sigma) } }) data <- list(y = MASS::newcomb) inits <- list(mu = 0, sigma = 5) constants <- list(n = length(data$y)) model <- nimbleModel(code = code, data = data, constants = constants, inits = inits)
Next we’ll create some vectors of node names that will be useful for our manipulations.
## Ensure we have the nodes needed to simulate new datasets dataNodes <- model$getNodeNames(dataOnly = TRUE) parentNodes <- model$getParents(dataNodes, stochOnly = TRUE) # `getParents` is new in nimble 0.11.0 ## Ensure we have both data nodes and deterministic intermediates (e.g., lifted nodes) simNodes <- model$getDependencies(parentNodes, self = FALSE)
Now run the MCMC.
cmodel <- compileNimble(model)
mcmc <- buildMCMC(model, monitors = parentNodes)
## ===== Monitors ===== ## thin = 1: mu, sigma ## ===== Samplers ===== ## conjugate sampler (2) ## - mu ## - sigma
cmcmc <- compileNimble(mcmc, project = model)
samples <- runMCMC(cmcmc, niter = 1000, nburnin = 500)
## |-------------|-------------|-------------|-------------| ## |-------------------------------------------------------|
Posterior predictive sampling by direct variable assignment
We’ll loop over the samples and use the compiled model (uncompiled would be ok too, but slower) to simulate new datasets.
nSamp <- nrow(samples) n <- length(data$y) ppSamples <- matrix(0, nSamp, n) set.seed(1) for(i in 1:nSamp){ cmodel[["mu"]] <- samples[i, "mu"] ## or cmodel$mu <- samples[i, "mu"] cmodel[["sigma"]] <- samples[i, "sigma"] cmodel$simulate(simNodes, includeData = TRUE) ppSamples[i, ] <- cmodel[["y"]] }
Posterior predictive sampling using values
That’s fine, but we needed to manually insert values for the different variables. For a more general solution, we can use nimble’s values function as follows.
ppSamples <- matrix(0, nrow = nSamp, ncol = length(model$expandNodeNames(dataNodes, returnScalarComponents = TRUE))) postNames <- colnames(samples) set.seed(1) system.time({ for(i in seq_len(nSamp)) { values(cmodel, postNames) <- samples[i, ] # assign 'flattened' values cmodel$simulate(simNodes, includeData = TRUE) ppSamples[i, ] <- values(cmodel, dataNodes) } })
## user system elapsed ## 4.657 0.000 4.656
Side note: For large models, it might be faster to use the variable names as the second argument to values() rather than the names of all the elements of the variables. If one chooses to do this, it’s important to check that the ordering of variables in the ‘flattened’ values in samples is the same as the ordering of variables in the second argument to values so that the first line of the for loop assigns the values from samples correctly into the model.
Doing the posterior predictive check
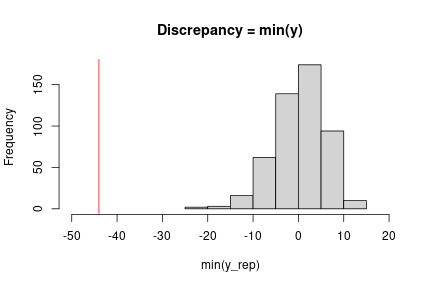
At this point, we can implement the check we want using our chosen discrepancy measure. Here a simple check uses the minimum observation.
obsMin <- min(data$y) ppMin <- apply(ppSamples, 1, min) # ## Check with plot in Gelman et al. (3rd edition), Figure 6.3 hist(ppMin, xlim = c(-50, 20), main = "Discrepancy = min(y)", xlab = "min(y_rep)") abline(v = obsMin, col = 'red')
Fast posterior predictive sampling using a nimbleFunction
The approach above could be slow, even with a compiled model, because the loop is carried out in R. We could instead do all the work in a compiled nimbleFunction.
Writing the nimbleFunction
Let’s set up a nimbleFunction. In the setup code, we’ll manipulate the nodes and variables, similarly to the code above. In the run code, we’ll loop through the samples and simulate, also similarly.
Remember that all querying of the model structure needs to happen in the setup code. We also need to pass the MCMC object to the nimble function, so that we can determine at setup time the names of the variables we are copying from the posterior samples into the model.
The run code takes the actual samples as the input argument, so the nimbleFunction will work regardless of how long the MCMC was run for.
ppSamplerNF <- nimbleFunction( setup = function(model, mcmc) { dataNodes <- model$getNodeNames(dataOnly = TRUE) parentNodes <- model$getParents(dataNodes, stochOnly = TRUE) cat("Stochastic parents of data are:", paste(parentNodes, collapse = ','), ".\n") simNodes <- model$getDependencies(parentNodes, self = FALSE) vars <- mcmc$mvSamples$getVarNames() # need ordering of variables in mvSamples / samples matrix cat("Using posterior samples of:", paste(vars, collapse = ','), ".\n") n <- length(model$expandNodeNames(dataNodes, returnScalarComponents = TRUE)) }, run = function(samples = double(2)) { nSamp <- dim(samples)[1] ppSamples <- matrix(nrow = nSamp, ncol = n) for(i in 1:nSamp) { values(model, vars) <<- samples[i, ] model$simulate(simNodes, includeData = TRUE) ppSamples[i, ] <- values(model, dataNodes) } returnType(double(2)) return(ppSamples) })
Using the nimbleFunction
We’ll create the instance of the nimbleFunction for this model and MCMC.
Then we run the compiled nimbleFunction.
## Create the sampler for this model and this MCMC. ppSampler <- ppSamplerNF(model, mcmc)
## Stochastic parents of data are: mu,sigma . ## Using posterior samples of: mu,sigma .
cppSampler <- compileNimble(ppSampler, project = model)
## Check ordering of variables is same in 'vars' and in 'samples'. colnames(samples)
## [1] "mu" "sigma"
identical(colnames(samples), model$expandNodeNames(mcmc$mvSamples$getVarNames()))
## [1] TRUE
set.seed(1) system.time(ppSamples_via_nf <- cppSampler$run(samples))
## user system elapsed ## 0.004 0.000 0.004
identical(ppSamples, ppSamples_via_nf)
## [1] TRUE
So we get exactly the same results (note the use of set.seed to ensure this) but much faster.
Here the speed doesn’t really matter but for more samples and larger models it often will, even after accounting for the time spent to compile the nimbleFunction.
Version 0.11.1 of NIMBLE released
We’ve released the newest version of NIMBLE on CRAN and on our website. NIMBLE is a system for building and sharing analysis methods for statistical models, especially for hierarchical models and computationally-intensive methods (such as MCMC and SMC).
Version 0.11.1 is a bug fix release, fixing a bug that was introduced in Version 0.11.0 (which was released on April 17, 2021) that affected MCMC sampling in MCMCs using the “posterior_predictive_branch” sampler introduced in version 0.11.0. This sampler would be listed by name when the MCMC configuration object is created and would be assigned to any set of multiple nodes that (as a group of nodes) have no data dependencies and are therefore sampled as a group from their predictive distributions.
For those currently using version 0.11.0, please update your version of NIMBLE. For users currently using other versions, this release won’t directly affect you, but we generally encourage you to update as we release new versions.
Version 0.11.0 of NIMBLE released
- added the ‘posterior_predictive_branch’ MCMC sampler, which samples jointly from the predictive distribution of networks of entirely non-data nodes, to improve MCMC mixing,
- added a model method to find parent nodes, called getParents(), analogous to getDependencies(),
- improved efficiency of conjugate samplers,
- allowed use of the elliptical slice sampler for univariate nodes, which can be useful for posteriors with multiple modes,
- allowed model definition using if-then-else without an else clause, and
- fixed a bug giving incorrect node names and potentially affecting algorithm behavior for models with more than 100,000 elements in a vector node or any dimension of a multi-dimensional node.
Please see the release notes on our website for more details.